1. série 10. ročníku

Dan našel u babičky na půdě krabici starých společenských her. Mezi nimi byly kostky domina nebo třeba šachovnice, která však byla podivně poničená, jak můžete vidět na obrázku.

Dana tedy napadlo, že se pokusí kostky domina na šachovnici vyskládat. Kolik kostek se Danovi povede na šachovnici položit tak, aby se nikde nepřekrývaly? Jedna kostka domina zabere přesně dvě sousední políčka šachovnice.

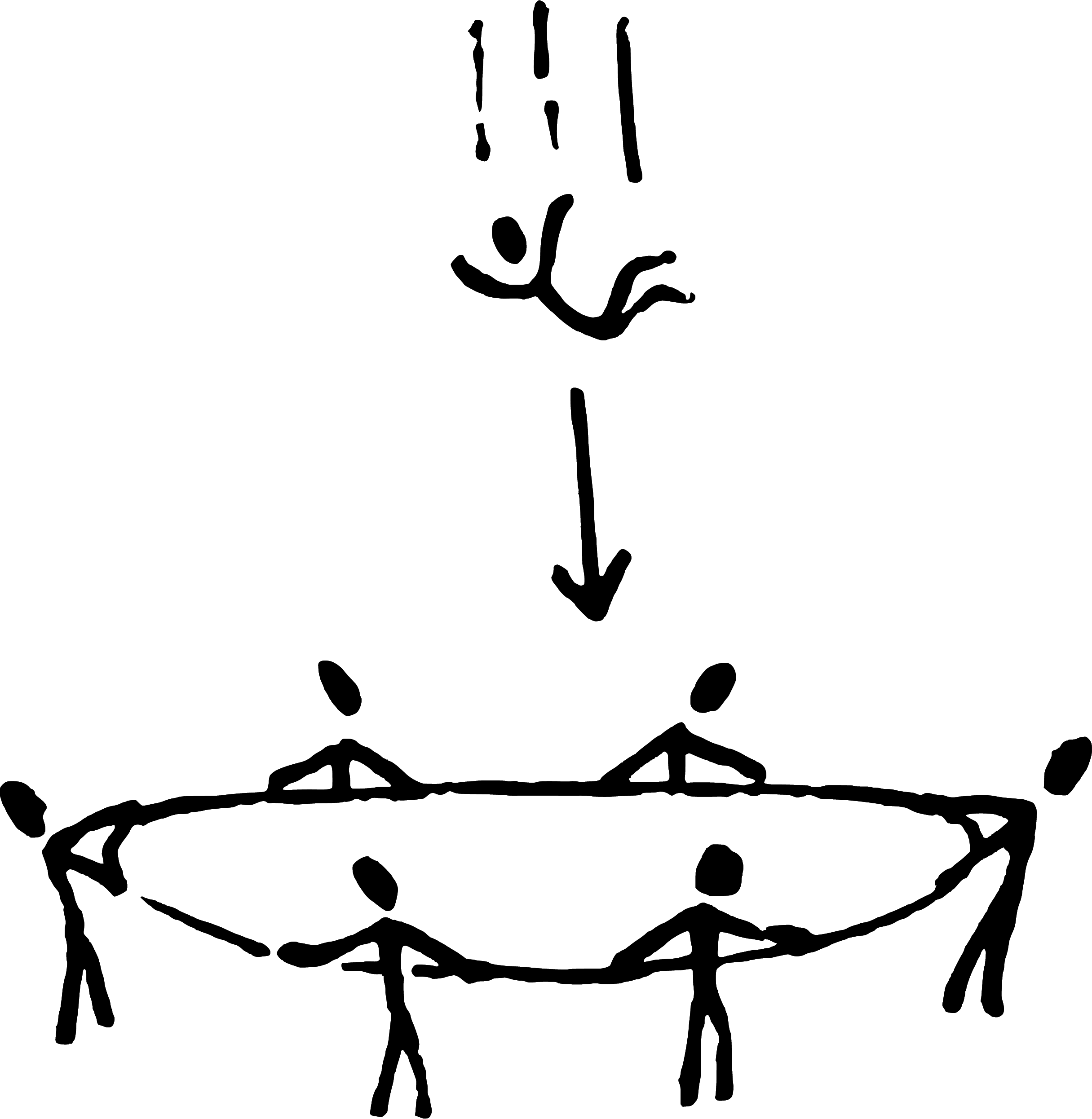
Během nácviku na natáčení musel kaskadér skákat ze třetího patra na kruhovou záchrannou plachtu, kterou napínalo dostatečně vysoko nad zemí kolem dokola několik jeho kolegů. Napnutá plachta má poloměr $3 \mathrm{m}$, a když zachytí kaskadéra v plné rychlosti, napne se ještě víc a můžeme si ji tehdy představit jako kužel o hloubce $1 \mathrm{m}$ s nezměněným obvodem (pružnost plachty dovoluje ji stále nehybně držet za okraj). Při testování plachty se zjistilo, že plachta je tak pružná, že ji skupina bez problému udrží, pokud se jí zvětší průměr ještě o $6 \mathrm{\%}$ od prvního napnutí.

Kaskadér se připravuje ke skoku, napětí roste a v dalším momentu už jen letí vzduchem. O zlomek sekundy později dopadá a rychle protahuje plachtu. Trhne to s pomocníky, nebo pád ustojí?

Jelikož se minulý ročník Výfuku vydařil, odměnil Výfuček organizátory pobytem v parádní chatě u hranic naší vlasti. Organizátoři velmi rychle zjistili, že chata má jímku o objemu $2 \mathrm{m^3}$, a co lepšího s jímkou dělat než sledovat její teplotu?

Dejme tomu, že každý organizátor se sprchuje přesně $40 \mathrm{l}$ vody. V jímce se po příjezdu nacházelo přesně $120 \mathrm{l}$ vody o teplotě $6 \mathrm{\C }$. Viktor dostal za úkol vypočítat předpokládanou teplotu, na které se ustálí voda v ní, jestliže se zimomřivá Soňa bude sprchovat vodou o teplotě $38 \mathrm{\C }$. Zajímalo ho také, kolik stupňů bude mít voda v jímce, jestliže se následně půjde sprchovat otužilý Marco, který má rád vodu o teplotě $6 \mathrm{\C }$. Pomozte Viktorovi vypočítat obě teploty za předpokladu, že teplo z vody se neuvolňuje jinam než do vody.

Matěj pak měřením ověřoval Viktorův předpoklad. Jakou teplotu by naměřil po Sonině sprše, jestliže se ve skutečnosti tepelné výměny účastnil i vzduch v jímce? Mohl naměřit rozdíl oproti teplotě vypočtené Viktorem, pokud jeho teploměr jako nejmenší dílky ukazuje desetiny stupně Celsia? Počítejte s tím, že před Soninou sprchou byla jímka se vzduchem v tepelné rovnováze. Měrná tepelná kapacita vody je $4 200 \mathrm{J\cdot kg^{-1}\cdot K^{-1}}$ a vzduchu $1 010 \mathrm{J\cdot kg^{-1}\cdot K^{-1}}$. Hustota vzduchu je $1,200 \mathrm{kg\cdot m^{-3}}$ a vody $1 000 \mathrm{kg\cdot m^{-3}}$.

Kapacita baterie v běžném chytrém telefonu činí alespoň $1 500 \mathrm{mAh}$ (miliampérhodin) při napětí zhruba $3,8 \mathrm{V}$. Kolik takových baterií je potřeba, pokud bychom s nimi s $60\%$ účinností poháněli elektrický jeřáb, kterým bychom se pokusili dostat klavír o hmotnosti $250 \mathrm{kg}$ do patra obytného domu ve výšce $20 \mathrm{m}$?

Výsledek vám uznáme i v případě, že místo uvedené kapacity použijete k výpočtu kapacitu, kterou si přečtete na baterii svého mobilu. Nezapomeňte však v tom případě pro systematičnost uvést váš model baterie a jeho výrobce.

Ve filmu Thunderball tajný agent James Bond využívá kapesní zařízení, které si vsadí do pusy a funguje jako žábry. Předpokládejme na chvíli, že takové zařízení skutečně existuje, a spočítejme si, jak moc by opravdu bylo použitelné.

1. Dospělý člověk se nadechne zhruba 15krát za minutu a na jeden nádech vdechne cca půl litru vzduchu. Jaký je v této úvaze průměrný tok $\Phi $ vzduchu do plic při nádechu (měřeno v $\mathrm{l/s}$)? Uvažujte, že nádech a výdech trvá zhruba stejně dlouho.
2. Obsah rozpuštěného kyslíku ve vodě je přibližně $\phi =8 \mathrm{cm^3/l}$, naproti tomu ve vzduchu je ho kolem $20 \mathrm{\%}$ objemu. Spočítejte, jaký tok kyslíku člověk potřebuje. Předpokládejme, že Bondovo zařízení dokáže dokonale a okamžitě oddělit rozpuštěný kyslík od vody. Jaký je potřebný tok vody Bondovým zařízením?
3. Filtrační zařízení bohužel nemá žádný pohon, který by jím proháněl vodu. Jak rychle by tedy James Bond musel plavat, aby zařízením proteklo dostatečné množství vody? Je takové zařízení reálné?

Předpokládejte, že Bond dýchá pusou o ploše $S=5 \mathrm{cm^2}$ a že díky železnému tréninku se mu při plavání nezvýší frekvence a hloubka nádechů. Pro nalezení rychlosti plavání můžete využít např. rozměrovou analýzu.

Mezi nejznámějšími vyvrácenými teoriemi v historii chemie je flogistonová teorie, která přežívala až do konce 18. století. Ta tvrdí, že každá hořlavá látka obsahuje směs tzv. flogistonu a popela. Během hoření flogiston uniká do okolí a ze směsi nakonec zůstane jen popel. Proto má například svíčka pod sklenicí obrácenou dnem vzhůru rychle zhasnout – dané množství vzduchu ve sklenici se flogistonuje (pojme flogiston) jen do určité nejvyšší míry a flogistonem nasycený vzduch pak brání úniku dalšího z místa hoření.

Za předpokladu, že je tato teorie správná, zkuste co nejpřesněji zjistit, jaký minimální podíl hmotnosti paliva (které je nutno určit) ve vašem krbu nebo grilu tvoří flogiston, resp. jaká jeho část unikne při vyhoření. Nemáte-li je k dispozici, můžete určit hmotnostní podíl flogistonu v dostatečně hmotné dřevěné třísce či špalku ze známého materiálu za improvizovaných podmínek. Pozor! Experiment provádějte venku (za dostatečného větrání) a na nehořlavém podkladu (kovová deska, písek, ohniště) pod dozorem dospělého! Nezapomeňte na důležitou diskusi nepřesnosti vašich měření.

Bonus: Mají váš popel či vyhořelé sirky jiné magnetické vlastnosti než původní palivo? Vyzkoušejte si je magnetem! O těchto vlastnostech a také o vyvrácení flogistonové teorie budeme více psát ve vzorovém řešení.

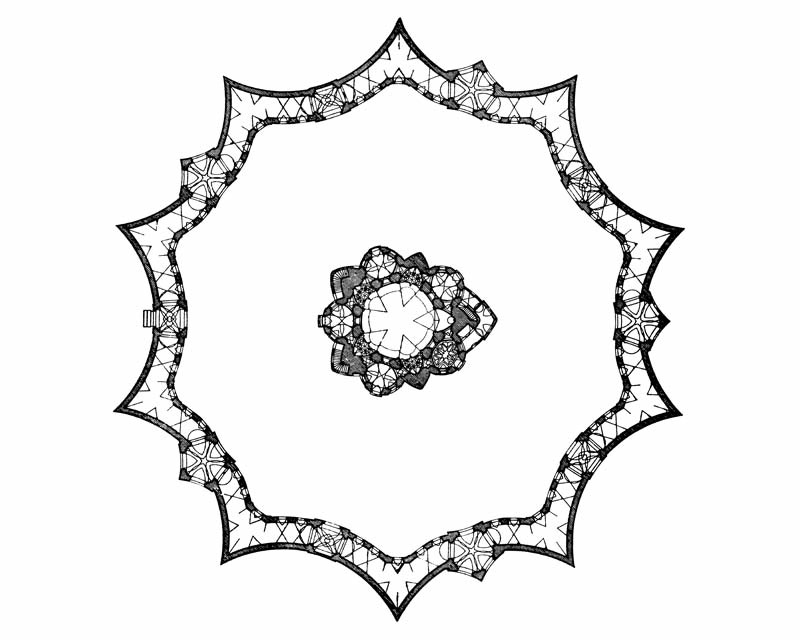
1. Český architekt Jan Blažej Santini proslul svými stavbami, ve kterých hojně užíval symetrií a numerologie. Zaměřme se na to, jakým způsobem Santini využil symetrií při stavbě proslulého kostela sv. Jana Nepomuckého na Zelené hoře. Nalezněte a popište všechny rotační a zrcadlové symetrie vnější zdi kostela, kterou můžete vidět na přiloženém půdorysu (za různé rotační symetrie se považují i ty, které se liší úhlem pootočení). Do obrázku zakreslete i příslušné osy a středy symetrie (prvky symetrie).
2. Ve Výfučtení byla krátce zmíněna obdélníková krystalická mřížka. Vytvořte nákres této mřížky pro hrany $a$ a $b$, kde $b=2a$. Jaké symetrie tato mřížka má?