3. série 11. ročníku
Termín odeslání: 10. 1. 2022 20:00:00
1. Jít, či nejít?
Výfuček si jednoho krásného odpoledne vyrazil na procházku. Počasí se však bohužel může měnit i velmi nečekaně, a tak během Výfučkovy zpáteční cesty začalo pršet. Aby co nejméně zmokl, rozhodl se Výfuček běžet. Pomohl mu ale běh opravdu v tom, aby byl na konci své cesty méně mokrý? Svou odpověď zdůvodněte. Uvažujte i jiné faktory než jen to, že bude doma dříve.
Uvažujte, že prší celou dobu stejně silně. To znamená, že na danou jednotku plochy dopadá v celém průběhu deště neměnné množství vody.
2. Mozková smrt
V kuchyni na Výfučím táboře se kuchařky rozhodly, že si uspořádají filmovou noc velmi špatných filmů. Tak špatných, že při jejichž sledování umírají mozkové buňky. Na začátku měla každá ze 4 přítomných organizátorek 100 000 000 000 mozkových buněk. Nejprve se promítal film dlouhý 35 minut s poločasem rozpadu mozkových buněk 5 minut a 50 sekund. Následoval film dlouhý 27 minut s poločasem rozpadu 2 minuty a 42 sekund, film dlouhý 55 minut s poločasem rozpadu 9 minut a 10 sekund, film dlouhý 39 minut s poločasem rozpadu 3 minuty a 15 sekund a na závěr si v kuchyni pustily film dlouhý 62 minut s poločasem rozpadu 15 minut a 30 sekund.
Zůstane na konci filmové noci v kuchyni dohromady alespoň jedna mozková buňka, kterou by kuchařky mohly sdílet?
3. Sypká věž
Organizátoři Výfuku si uspořádali párty. Podmínkou ke vstupu na párty bylo přinést alespoň litr sypké substance.
Kačka přinesla litr popela, který má sypný úhel 20∘. Viktor přinesl litr mletého kakaa, které má sypný úhel 30∘. Marco přinesl litr práškové křídy, která má sypný úhel 45∘.
První vysypali hromádku popela, ta měla tvar komolého kužele, tedy kužele s useknutou špičkou. Splácli ji takovým způsobem, aby na ni mohli vršit kakao. Styčné plochy mezi jednotlivými sypkými látkami jsou vždy jen vodorovné. Prostřední hromádka kakaa má také tvar komolého kužele a na ní je umístěn kužel z práškové křídy.
Jak (nejvíce) vysoká může být tato hromádka?
4. Hodiny se šiškami a kukačkou
Viktor má na chatě hodiny se čtyřmi šiškami, z nichž každá váží m=0,5 kg. Jak dlouho po natažení budou hodiny fungovat, pokud mohou obě šišky klesnout až o l=1 m a pro pohon hodin je použitelných 20 % potenciální energie šišek? Hodiny mají hodinovou ručičku dlouhou 6 cm a vážící 15 g, minutovou ručičku dlouhou 7 cm a vážící 10 g a konečně sekundovou ručičku, která měří 8 cm a váží 5 g.
Ručičky hodin považujte za homogenní zanedbatelně tenké tyče a předpokládejte, že hodinový strojek na ně působí pouze během jejich pohybu od šestky ke dvanáctce. Také pro jednoduchost můžete učinit odhad, že během 12 hodin spotřebovávají ručičky energii lineárně. Hodiny Viktor natáhne přesně v poledne.
5. Nedostavěný obchvat
Město Výfučkov leží na hlavní cestě mezi Prahou a Brnem, tedy většina aut, která jím projíždí, se snaží dostat ze severu na jih. Bohužel však městem protéká ve směru z východu na západ řeka.
Aby auta nejezdila městem, rozhodli se ve Výfučkově stavět obchvat. Jelikož se ale zastupitelé severní a jižní části nedohodli, začali ze severu stavbu obchvatu západním směrem a z jihu začali stavět z východní strany, přičemž oba obchvaty dostavěli až po most přes řeku (starý most v centru během stavebního šílenství strhla povodeň). Pro průjezd ze severu na jih tedy zbyly dvě možnosti, využívající vždy na jednom břehu obchvat a na druhém průjezd městem.
Každá část obchvatu je kapacitní a cesta po ní trvá 30 minut bez ohledu na to, kolik aut ji využívá. Druhou část cesty však řidiči musí jet městem, kde cesta trvá 4 minuty za každých 100 aut, které po dané silnici projíždějí jedním směrem.
- Městem každé ráno projíždí jedním směrem 1 000 aut, jejichž řidiči mají chytré navigace, tedy si každý z nich zvolí nejvýhodnější cestu včetně dopravního vytížení: buď obchvatem a pak městem z jedné strany, nebo městem a pak obchvatem z druhé strany (most přes řeku město-město pro auta neexistuje). Jak dlouho bude každému řidiči trvat průjezd městem? Nakreslete si diagram cest.
- Nový primátor se rozhodl části usmířit, dopravní situaci vyřešit a vybudovat tunel, který nedostavěné části obchvatu propojí. Tato vymoženost dokonale spojuje cesty v půlce města: tedy když auto začne jet po obchvatu, může pokračovat běžně městem, nebo projet tunelem na druhou část obchvatu. Ale i když začne cestu městem, může se v půlce rozhodnout, jestli bude pokračovat po obchvatu jako běžně, nebo projede tunelem a zase pojede městem. Průjezd tunelem trvá 3 minuty bez ohledu na to, kolik aut jím projíždí. Jak dlouho bude nyní každému řidiči trvat nejvýhodnější trasa?
- Výfuček se rozhodl primátorovi ukázat, co svou iniciativou provedl, a to jak jinak než pomocí fyzikálního modelu. Vzal tedy dvě pružinky o tuhosti k=0,25 N⋅cm−1 a počáteční délce téměř nulové, na každou navázal provázek dlouhý 30 cm a pružinky propojil provázkem dlouhým 3 cm. Sestava tedy odpovídala městským cestám, kde provázky jsou tunel/obchvat a pružinky cesta městem. Na obě pružinky zároveň pak Výfuček pověsil závaží působící silou 10 N. Jaká bude vzdálenost závaží od bodu závěsu? Nejspíš budete muset použít vztah pro skládání tuhosti dvou sériově visících pružinek.
- Výfuček poté vzal nůžky a krátký provázek 3 cm přestřihl. Co se stalo se závažím? Jak tato situace odpovídá dopravní situaci popsané výše (tj. které „pružinkové“ veličiny odpovídají kterým dopravním)?
Předpokládejte, že pružinky mají nulovou klidovou délku.
E. Cinknutá kostka
Baví vás hrát Člověče, nezlob se? Většina lidí odpoví ano, jen když zrovna vyhrává. K výhře však potřebujeme pořádnou dávku štěstí. A nebo si to štěstí můžeme nějak pojistit…
Vyrobte si tzv. cinknutou kostku, na které padají šestky častěji než ostatní čísla. Kostka by ale neměla být moc nápadná, těžko by si s vámi někdo zahrál, kdyby neházela nic jiného než šestky. Pokuste se proto, aby relativní četnost hození šestky (podíl počtu hodů, kdy padla šestka, a počtu všech hodů) byla co nejblíže \textbf {jedné třetině}. Jednička by měla naopak padat co nejméně.
Můžete jak upravit obyčejnou kostku, tak od základu vytvořit novou (např. z papíru). Pečlivě popište svůj postup výroby i výslednou stavbu kostky a změřte relativní četnost hození jednotlivých čísel. Je pro hodnoty mimo šestku a jedničku vaše kostka spravedlivá?
K následující úloze se vztahuje i tzv. Výfučtení. To můžeš nalézt v naší brožurce výše.
V. Záření hvězd
- Chemici nalezli ve spektru čáru H-epsilon – přechodem elektronu mezi kterými hladinami vznikla tato čára? Vypočtěte pomocí Balmerova vzorce, na jaké vlnové délce tuto čáru v laboratorních podmínkách najdeme. Dále spočtěte, jakou energii má foton vyzářený tímto přechodem.
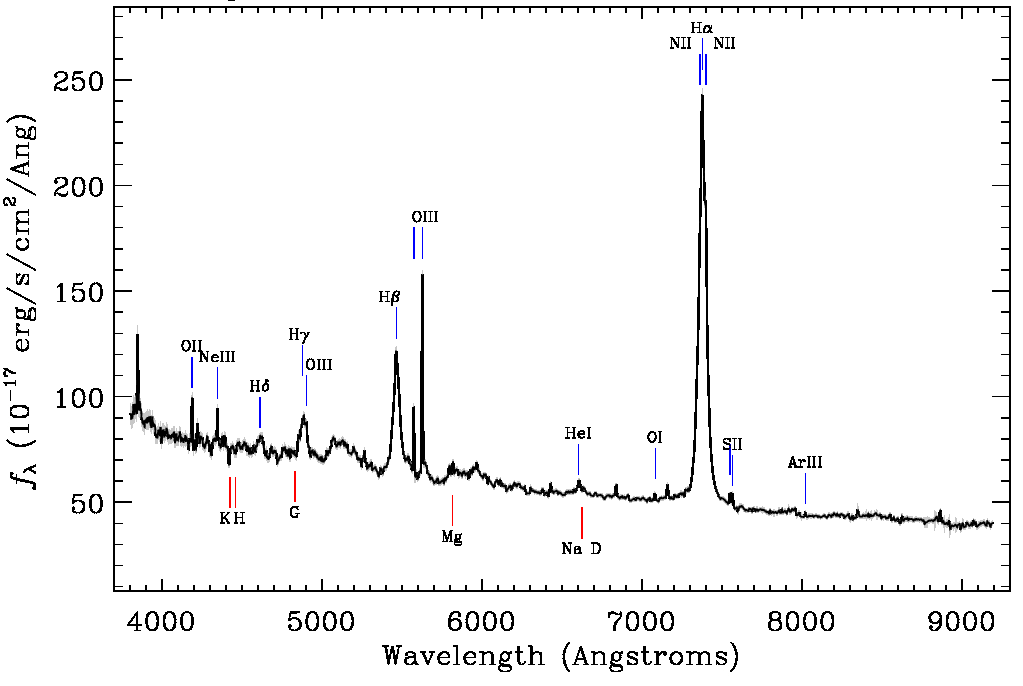
- Astronomové pozorovali vzdálenou galaxii a získali spektrum, které vidíte na obrázku. Na jaké vlnové délce najdeme čáru H-alpha? Pomozte astronomům spočítat radiální rychlost dané galaxie, když víte, že laboratorní vlnová délka čáry H-alpha je λ0=656 nm. Pohybuje se galaxie směrem od nás, nebo se přibližuje?
Přestože to pro řešení této úlohy není důležité, povšimněte si veličiny na svislé ose. Základní veličinou observační astronomie je intenzita, která udává výkon záření na jednotku plochy pozorovacího přístroje a jednotku vlnové délky nebo frekvence, pro danou úhlovou výseč zdroje. Například kolik wattů přichází na metr čtvereční na nanometr z dané úhlové výseče Slunce.
Zde je na svislé ose vynesena hustota zářivého toku, což je výkon vztažený na jednotku plochy a vlnové délky, ale z celého zdroje – není tedy vztažena na jednotku prostorového úhlu. V astronomii se někdy setkáme s neobvyklými jednotkami. Jedná se o pozůstatek soustavy cgs (centimetry-gramy-sekundy), která bývala v experimentální fyzice po dlouhou dobu používána.
Jednotkou energie v cgs soustavě je erg, který odpovídá 10−7J. Vlnová délka se někdy měří v jednotce zvané Angström, což je 10−10m, tedy desetina nanometru. Za jednotku plochy byl zvolen čtvereční centimetr.