2. série 11. ročníku
Termín odeslání: 29. 11. 2021 20:00:00
1. Rovnovážná
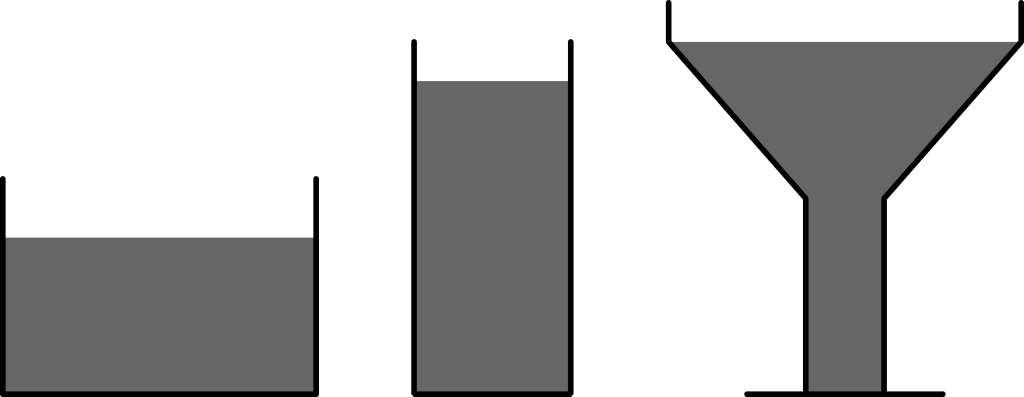
Na obrázku můžete vidět tři různé nádoby. Která z nich má nejvyšší stabilitu, tedy kterou z nich je nejtěžší převrhnout? Rozměry nádob pro potřeby výpočtu odhadněte. Nádoby jsou osově symetrické, tedy např. první nádoba je válec. Připomínáme, že pro určení stability lze použít např. veličinu stabilita, která je definovaná jako rozdíl potenciální energie labilní a aktuální polohy.
2. Rychlé čtení

Kačka s Evou jednou porovnávaly, jak rychle dokáží číst v různých jazycích. Kačce trvá přečtení jedné stránky anglicky dvakrát tolik minut co přečtení jedné stránky česky a přečtení jedné stránky francouzsky dvakrát tak dlouho co anglicky. Eva čte všemi jazyky stejně rychle. Přečtení textu o jedné české a jedné anglické stránce trvá oběma stejně dlouho, a to 3 minuty. Jednou dostaly za domácí úkol přečíst českou knížku o 250 stránkách, anglickou o 100 stránkách a francouzskou o 50 stránkách. Která bude mít knížky přečtené rychleji?
3. Psaní slohovky
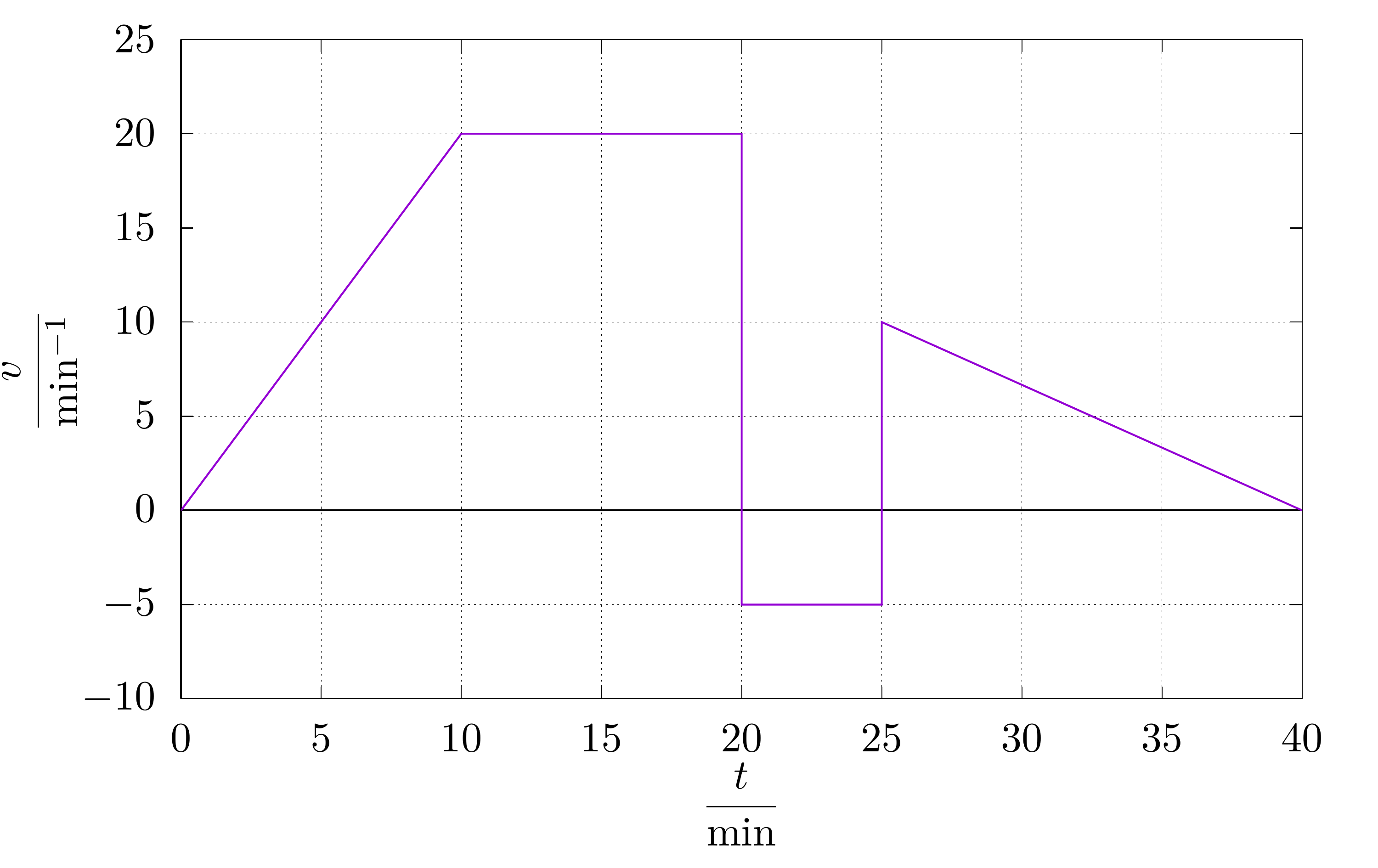
Adam se snažil napsat slohovou práci o minimálním počtu 250 slov. Rychlost, s jakou ji psal, je znázorněna v grafu. Kdy Adam dosáhl potřebného počtu slov a kolik jich měl po dopsání?
4. Tepelné čerpadlo

Viktor si chce pořídit na chatu nové bazénové tepelné čerpadlo. Zajímá ho však, za jak dlouho se investice do něj vrátí. Tepelné čerpadlo, které si vybral, stojí 24 000Kč, má příkon 1 kW a tepelný výkon 6,8 kW. Bazén má objem 20 m3 a 1 kWh elektřiny stojí 4 Kč. Předpokládejte, že Viktor chce typicky svůj bazén ohřát o 5 ∘C, aby Luborovi nebyla zima, a za rok pořádá v průměru dvacet bazénových párty.
Situaci porovnávejte s případem, kdy by Viktor bazén vytápěl přímo pomocí elektřiny ze sítě se 100% účinností.
5. Lukáš vaří

Lukáš se rozhodl připravit si k obědu instantní čínskou polévku. Na obalu si přečetl, že obsah pytlíku má vhodit do jednoho litru vařící vody. Naštěstí si ale včas uvědomil, že kdyby na plotnu postavil hrnec s jedním litrem vody, dopustil by se osudové chyby, neboť by vody připravil příliš mnoho. Kvůli teplotní roztažnosti by se totiž objem vody během ohřívání zvětšil, a tak by jí po dosažení teploty 100 ∘C bylo více než 1,0 l.
- Kolik vody by měl tedy odměřit, aby jí v hrnci po ohřátí byl právě jeden litr, pokud mu z kohoutku teče voda o teplotě 20 ∘C? Počítejte s neměnným koeficientem teplotní objemové roztažnosti β=190 ⋅ 10−6 K−1.
- Lukáš ale zjistil, že doma bohužel nemá vhodnou odměrku, aby mohl takovéto množství odměřit. Napadlo ho však alternativní řešení. Do hrnce odměří 1, l vody, následně vodu ohřeje a poté chvilku počká až se přebytečné množství odpaří, aby mu v hrnci zbyl kýžený jeden litr. Jak dlouho od dosažení bodu varu bude muset počkat, než se přebytečné množství odpaří, pokud má jeho sporák výkon 3,0 kW?
E. Poločas čočky
Experimenty s radioaktivitou, o kterých se můžete dočíst ve Výfučtení, jsou pro provedení doma příliš nebezpečné. Můžeme si však radioaktivní rozpad namodelovat pomocí čočky. Vezměte si několik zrnek kuchyňské čočky (doporučujeme alespoň 200) a na každou z nich namalujte na jednu stranu tečku. Poté čočku rozsypte a separujte a spočítejte zrnka s tečkou nahoře, která reprezentují rozpadlé atomy. Postup několikrát opakujte, ideálně dokud vám zbývají „nerozpadlá“ zrnka. Poté sestavte graf závislosti počtu nerozpadlých jader na počtu hodů, do kterého kromě naměřených hodnot vyneste i předpokládaný průběh experimentu. Abyste zjistili, zda je takovýto rozpad konsistentní, můžete jej samozřejmě opakovat.
Jaký je poločas rozpadu čočky? Modeluje čočka radioaktivní rozpad věrohodně? Pokud zjistíte výrazné odchylky od předpokládané závislosti, diskutujte, čím by mohly být způsobeny. Místo čočky lze samozřejmě použít cokoliv symetrického, například jednokoruny či bonbóny Skittles.
K následující úloze se vztahuje i tzv. Výfučtení. To můžeš nalézt v naší brožurce výše.
V. Jádro pudla
- Existují jaderné reaktory, které místo štěpení směsi uranových izotopů štěpí jádra 239Pu. Jednou z reakcí, které v reaktoru probíhají, je
239Pu+1n−>234U+4He+21n .
Určete, kolik energie se během reakce vyprodukuje. Toto číslo srovnejte s energií, kterou vyprodukovala reakce popsaná ve Výfučtení.
- Po spotřebování veškerého vodíku dochází ve hvězdách k fúzi vzniklých jader helia a to podle rovnice
3He+4He−>7Be .
Vaším úkolem je zjistit, jaká energie se uvolňuje během této reakce. Také porovnejte uvolněnou energii z reakce s energií uvolněnou sloučením vodíkových jader.
- V medicíně využíváme izotop 18F, a to ke zjišťování rozsahu šíření rakoviny v těle. Ten se vyrábí jadernou reakcí
18O+1H−>18F+1n . Určete, zda se jedná o reakci energii spotřebovávající, nebo produkující, a případně kolik energie se uvolní nebo kolik energie musíme reakci dodat, aby proběhla.
Potřebné údaje si vyhledejte na internetu, např. v odkazu uvedeném ve Výfučtení.