2. série 10. ročníku
Termín odeslání: 7. 12. 2020 20:00:00
1. Vrt
Už vás někdy napadlo, co leží pod Českem – přesně na druhé straně Země? Představme si vrt vedený z České republiky přes střed Země na druhou stranu. Jaké zeměpisné souřadnice bude mít bod na konci vrtu a jak se nazývají geografická místa poblíž onoho bodu? Předpokládejte, že vrt provádíme na zeměpisné šířce 50∘ s. š. a zeměpisné délce 15∘ v. d. Jak by se výsledek změnil, pokud byste začali kopat na souřadnicích svého bydliště?
2. Stará televize
Organizátoři Výfuku se o prázdninách vydali k Viktorovi na chatu. Když tam dorazili, zaujala Kačku stará televize natolik, že se zamyslela nad tím, jak vlastně funguje. Obrazovka televize má rozměry 25 cm×25 cm a zobrazuje obraz pomocí paprsku urychlených elektronů. Ty dopadají na povrch stínítka pokrytý luminoforem, který po dopadu elektronů vydává světlo. Předpokládejme, že obrazovka se rozdělí na 625 řádků, kterými potřebuje paprsek probíhat tak rychle, abychom viděli souvislý obraz, tedy aby paprsek tvořil 25 snímků za sekundu. Pomozte Kačce spočítat, jakou nejmenší rychlostí se mohl konec paprsku pohybovat po stínítku.
3. Rozštípená skála

Organizátoři Výfuku se vydali na krátký výlet po okolí Hamrů nad Sázavou. Jejich cílem se stala Rozštípená skála – skalní útvar, který podle pověsti vznikl s přispěním ďábla. Jeho asistence spočívala v tom, že jednak uvolnil rulový skalní blok 10×10×2 metry, jednak puklinu rozevřel až do šířky dva metry. Toto učinil pomocí neznámého množství dynamitu. 30 % uvolněné chemické energie bylo spotřebováno na oddělení skály, zbylých 70 % na posunutí odděleného bloku – ďábel samozřejmě pracuje s dokonalou efektivitou. Odhadněte, kolik dynamitu použil, jestliže podloží kladlo pohybu bloku odpor 5 MN.
4. Luborovi je zima
Po návratu z výletu se organizátoři rozhodli, že se půjdou koupat. Lubor ale nemá rád studenou vodu a do zahradního bazénu, který měl teplotu 28 ∘C, se mu příliš nechtělo. Proto si musel počkat do druhého dne, kdy se bazén během dne díky průhlednému zakrytí ohřál o 2 ∘C. Kolik hodin muselo nejméně svítit, jestliže právě polovina sluneční energie dopadající na průhledný kryt o povrchu 6 m2 byla využita k ohřevu vody v bazénu? Výsledek srovnej s časem, za který by bazén ohřálo tepelné čerpadlo s výkonem 4 kW. Nakonec můžeme prozradit, že bazén obsahoval 8 m3 vody a ostatní potřebné hodnoty je třeba dohledat.
5. Výlet balónem
Přátelé Výfuku se jali létat balónem. Avšak báli se, že uletí a dojde jim kyslík, a proto přivázali balón na pružinu, která byla pevně spojena se zemí, a začali kmitat. Nenatažená pružina měla délku l0=150 m a nejvýše nad povrchem Země byli ve výšce h=160 m. Balón, naplněn vzduchem o hustotě ρ=0,90 kg⋅m−3, měl objem V=2500 m3. Hmotnost balónu a lidí v něm byla m=800 kg. Běžná hustota vzduchu za normálního tlaku a teploty je ρ0=1,29 kg⋅m−3.
1. Jak velkou vztlakovou silou byl balón nadnášen?
2. Jakou celkovou silou F balón natahuje pružinu, je-li ve výšce l0?
3. Pokuste se určit tuhost použité pružiny. Napovíme vám, že pro tuhost pružiny k platí: F=kΔl=k(l−l0) , kde F je síla, která natahuje pružinu, l je délka natažené pružiny a l0 je délka pružiny v klidu.
4. S jakou frekvencí balón kmitá? Pro frekvenci kmitavého pohybu platí: f=12π√kgF , přičemž k vyjadřuje tuhost pružiny, g tíhové zrychlení a F je síla natahující pružinu.
E. U-rampa
Organizátoři Výfuku se rozhodli, že si zajdou na minigolf. Při hraní si všimli, že na různé dráhy se hodí různé vlastnosti míčku a že záleží na tom, jak se k jamce odpálí.
Zkuste si i vy v různých případech prozkoumat chování materiálu. Zkonstruujte si doma U-rampu ve tvaru půlkruhu s minimální výškou 10 cm (například z kartonu a drátků nebo ohnuté matrace). Poté si sežeňte několik malých kuliček z různých materiálů (například hopík, železnou kuličku či kuličku od myši) a pouštějte je z vrcholu rampy. Změřte, do jaké výšky jsou schopné kuličky na druhé straně rampy vyjet. Se stejnými míčky pak změřte i to, jak vysoko se odrazí, když je pustíte na zem ze stejné výšky, z jaké jste je pouštěli na U-rampě.
Porovnejte ztrátu energie při průjezdu rampou a při odrazu pro vaše kuličky. Ztrátu energie můžete popsat vydělením výsledné potenciální energie energií počáteční. V případě pádu podíl nazýváme koeficient restituce (neboli účinnost). Čím jsou rozdíly ve ztrátě energie způsobeny? Nezapomeňte, že čím vyšší dráhu zvolíte, tím přesnější výsledky obdržíte.
K následující úloze se vztahuje i tzv. Výfučtení. To můžeš nalézt v naší brožurce výše.
V. Mezi ploty
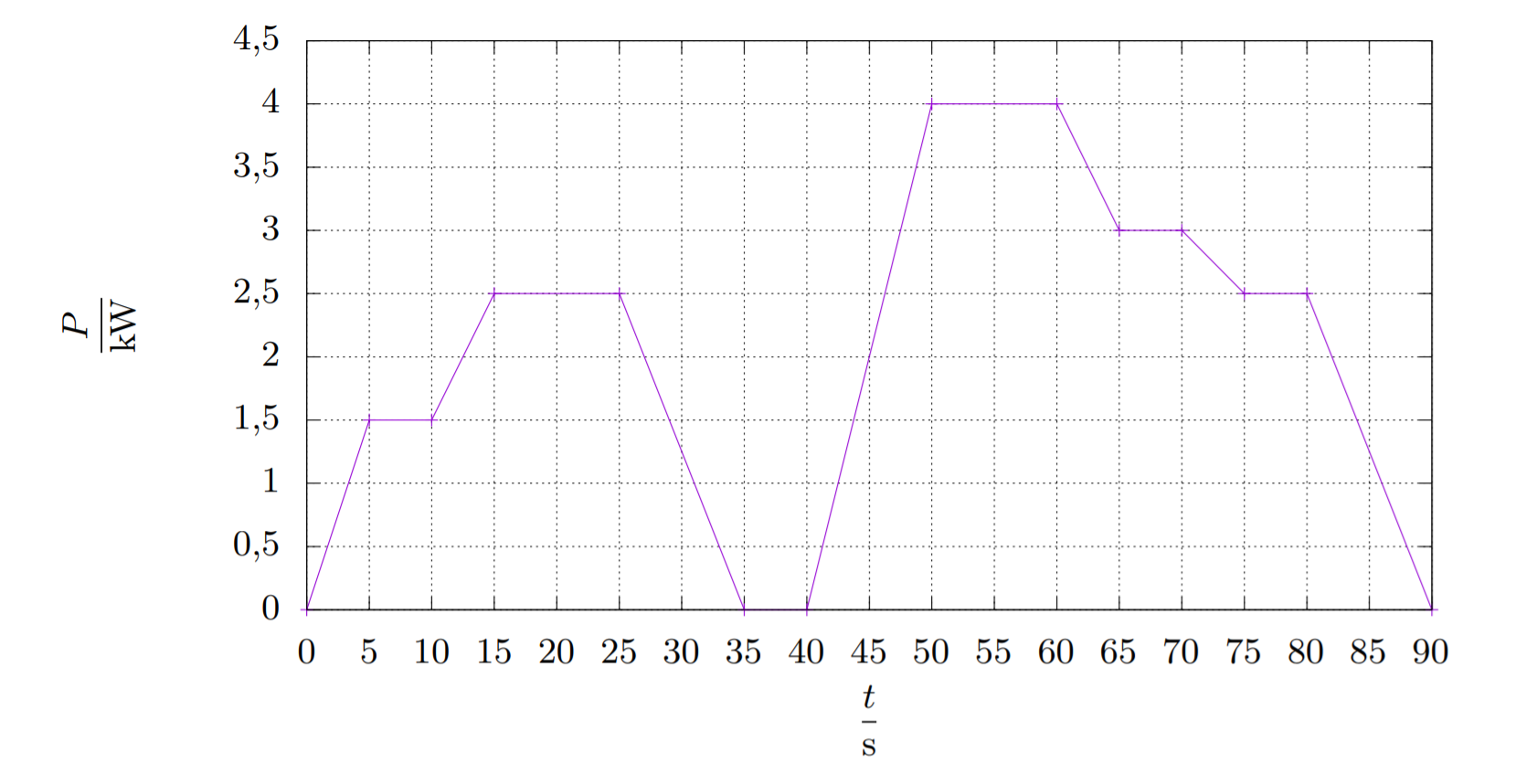
Obr. 2: Průběh odebíraného výkonu navijáku v čase

Obr. 1: Dobře čitelný graf
- Na přiloženém grafu na obr. 1 si můžeme demonstrovat, jak je důležité, aby údaje v něm byly čitelné. Odstranili jsme souřadnicovou mřížku a zvolili nevhodné měřítko a značení os. Určete graficky, jaká byla hodnota veličiny b pro hodnotu závislé veličiny a=−0,7.
- V dalším grafu na obr. 2 si můžete prohlédnout časový průběh elektrického výkonu navijáku, kterým jeřábník na staveništi zvedal betonový panel o hmotnosti m=1000 kg při tíhovém zrychlení g=9,8 m⋅s−2. Do jaké výšky jej zvednul?
Nápověda: Elektrická práce je definována jako součin dvou veličin stejně jako dráha v kinematice. Můžeme s ní tedy pracovat obdobně, pomůže nám rozměrová analýza. - Zaznamenejte si v průběhu jednoho týdne, kolik hodin či minut jste strávili každý den nějakou častou činností dle vašeho výběru – prací do školy, díváním se na televizi, používáním mobilu, kontaktem s kamarády, nebo čímkoli jiným. Vytvořte závislost stráveného času na kalendářním datu, ale graf nekreslete. Naopak vytvořte jej v alespoň jednom počítačovém systému zmíněném ve Výfučtení. Systém si můžete vybrat sami a nezapomeňte na to, aby byl graf čitelný a měl všechny náležitosti. Můžete jej připojit jako obrázek do PDF či vytisknout k řešení zasílanému poštou a napsat, který program jste zvolili.