Hokus Pokus: Jak na experimentální úlohy
- Krátká taháková verze textu (poslána poštou)
Nenechte se odradit rozsahem textu, slouží též jako úvod do experimentální fyziky jako takové. Pro referenci také stačí používat „tahák“ odkázaný výše.
Úvod
Každá série Výfuku obsahuje experimentální úlohu, v níž je obvykle úkolem využít svých fyzikálních znalostí k stanovení hodnoty předem dané veličiny, kterou popisujeme nějaký skutečný jev.1) Takový úkol obvykle vyžaduje sestavit fyzikální pokus (experiment), kde by mohla být daná veličina číselně určena (naměřena). Znalost teoretické fyziky nutná pro odůvodnění použitého experimentálního postupu není ještě dostačující pro vyřešení úlohy, nepřidá-li se k ní také znalost správného vypracování výstupu experimentu. V průběhu historie fyziky (ale i chemie) se ukázalo, že existuje jeden nejužitečnější postup, jenž dnes dodržují i vyžadují vědci ze všech oborů, ve kterých je úkolem zjišťovat nějaká čísla (přejali jej technici, sociologové, lékaři a mnozí další), a který nám umožňuje z experimentu zaznamenat vše důležité tak, aby mohl být interpretován a zopakován někým jiným. Taková je motivace pro důkladné vypracování experimentální úlohy. Opakované měření se stejnými výsledky může totiž být důkazem teorie, a dokud se to nepodaří, zpravidla se výsledky nějakého experimentu mezi vědci považují za ještě „nepotvrzené“.2)
Zmiňovaný postup spočívá v poctivém zpracování (sepsání) následujících kapitol; byli bychom rádi, kdybyste vaše řešení strukturovali přibližně tak, jak je rozebírá text níže:3)
- Teorie nebo též Teoretický úvod: obsahuje úvahu nad vhodným měřením a vzorce použité k určení výsledků z naměřených hodnot.
- Experiment: obsahuje popis použitého pokusu nebo zařízení, na kterém je pokus prováděn, spolu s měřicími přístroji jako doklad, že jste experiment provedli a jak. U experimentů, u kterých je to důležité, je třeba napsat i okolní podmínky (např. okolní teplotu nebo počasí).
- (Výsledky/Zpracování) měření (může být součástí předchozí kapitoly): tato kapitola je nejzajímavější, protože obsahuje jak vaše experimentálně zjištěná data (jejich tabulky, grafy apod.), tak z nich vypočtené výsledné hodnoty, a co je velmi důležité, i vyhodnocení nejistot těchto výsledků (jak přesné jsou, jakou mají odchylku od skutečnosti apod.).
- Závěr nebo Diskuze: Poslední část by měla shrnovat získané odpovědi podobně, jako je tomu v matematice při řešení slovních úloh s napsáním výsledku v celé větě. Shrnuje také kvalitu měření, získané výsledky i jejich přesnost a může je porovnávat s tabulkovými či navrhovat, jak experiment zlepšit.
Jen ten, kdo ve svém řešení obsáhne vše důležité ze zmíněných kapitol, dostává plný počet bodů. Tento materiál má sloužit nejen jako pomůcka k vypracování úloh ve Výfuku, ale měl by vám také pomoci zpracovat jakýkoliv jednodušší experiment, ať už to bude na našem táboře, ve škole, ve fyzikální olympiádě či jiné soutěži. Je ale nutné pamatovat na to, že každý experiment je odlišný a na jeho zpracování se mohou hodit i jiné metody. I když se následující pojednání může zdát složité, v doporučeném postupu rychle získáte praxi.
Teorie
V první části jednoduše popíšeme úvahu, na které bude provedení našeho experimentu založeno. Jeho nedílnou součástí jsou vzorce, ze kterých budeme určovat výsledné hodnoty závisející na měřených veličinách. Ve správné vědecké práci se zde vedle výpočtů výsledných hodnot uvádějí i metody výpočtu nejistot, tedy vyčíslení přesnosti těchto hodnot.4) U některých, na provedení jednodušších experimentů je někdy možné určovat hledané hodnoty rovnou bez výpočtů. V tomto smyslu se liší tzv. přímé a nepřímé měření. Každé nepřímé měření (např. měření síly metodou využívající výpočtu F=ma) sestává ze zpracování výsledků jednotlivých přímých měření (např. určení jednotlivé hmotnosti a zrychlení pro dosazení do zmíněného vzorce).
Ještě před tím, než začnete měřit, se musíte na měření připravit. Důležitá součást provedení experimentu, která zlepší kvalitu vaší práce, je jeho promyšlení. Ujasněte si, jakou veličinu vlastně budete měřit a jaké veličiny budete potřebovat k jejímu určení. V případě více možných metod si vyberte tu, kterou dokážete odvést nejpřesněji. Pokud měříte nějaký periodicky se opakující děj (například dobu kyvu kyvadla nebo délku kroku), můžete pro zlepšení přesnosti měřit např. součet desíti těchto dějů po sobě proběhlých a poté výsledek vydělit deseti (tím zmenšíte nepřesnost v určení času, která plyne z vaší reakční doby); nebo pokud měříte hmotnost něčeho velmi lehkého či tloušťku něčeho velmi tenkého a vaše váhy či měřidla nedokáží rozlišit tak malé hodnoty, naskládejte toho k sobě víc a výsledek určete analogicky. Někdy je šikovný trik klíčový ke správnému provedení měření.
Poslední věcí, kterou se před experimentem musíte zabývat, jsou pomůcky (popsané v další kapitole). Nezapomeňte si všechny potřebné a adekvátně přesné pomůcky předem obstarat a zvažte také vypůjčení si těch, které doma nemáte, třeba od vaší školy.
Experiment
Někdy je možno tuto kapitolu zpracovat už spolu s teorií, protože teorie a zvolená metodika experimentu spolu úzce souvisí. Není-li postup už přesně popsán v zadání úlohy, je dobré sdělit, jakých přesně nástrojů jste využili k měření nebo jak vypadalo zařízení, které bylo pro měření klíčové. Záznam vnějších podmínek je také důležitý, jde-li například o pokus závislý na teplotě, tlaku nebo jiných okolnostech. U měření astronomických je zásadní zaznamenat čas a místo pozorování a seznam bychom mohli takto stále zvětšovat. Jednoduše řečeno je třeba uvážit, co bude měření ovlivňovat a s čím musí počítat ten, jenž by po nás chtěl experiment zopakovat se svým vybavením.
Měřicí aparaturu nezapomeňte zdokumentovat. Vyfoťte si ji nebo načrtněte a obrázek ideálně připojte k řešení. Umožníte tak měření nejen reprodukovat, ale také si ostatní budou moci představit, jak probíhalo.
Výsledky a zpracování měření
Následuje klíčová část experimentální úlohy, a tou je prezentace naměřených dat spolu s jejich přesným zpracováním, které nám prozradí hledané výsledky. Vraťme se však ještě na chvíli k průběhu experimentu samotného, při němž se můžeme setkat s řadou různých okolností a které nám mohou někdy i záznam dat ztěžovat.
Pokud už máte všechny pomůcky k měření připravené a experiment důkladně rozmyšlený, můžete měřit. I potom je ale třeba postupovat s rozvahou. Nejprve se ujistěte, že máte dostatek času, abyste experiment neuspěchali. Může se pak stát, že zapomenete změřit nějakou nezbytnou hodnotu, nebo experiment jednoduše nestihnete dokončit.5) Měřit je také dobré „v jednom zátahu“, aby se rušivé vlivy pozadí příliš neměnily a vám vycházely konzistentní hodnoty. Najděte si dobré místo k měření tak, aby toto rušení bylo co nejmenší.6)
Vhodný způsob záznamu dat je také důležitý. Prostý papír často postačí, nicméně uvažujte o zapisování dat do počítače.7) Když budete měřit, kontrolujte si i v průběhu data, která jste naměřili. Pokud vám vychází řádově jinde, než očekáváte, zamyslete se nad tím, jestli jste se nedopustili tzv. hrubé chyby (například špatně provedený experiment, posunuté pravítko apod.). Pokud jste se hrubé chyby dopustili anebo vlivy prostředí byly obzvláště silné (například zafoukal vítr), chybnou hodnotu škrtněte a měření opakujte. Pokud máte doměřeno, zkontrolujte si alespoň letmo, jestli vám měření vychází tak, jak byste očekávali8) a pokud ne, máte ještě šanci experiment proměřit.
Po změření všech potřebných veličin máte skoro vyhráno, ale napsat na papír naměřené hodnoty a výsledek zdaleka nestačí (i když je nutné připravit jejich přehlednou tabulku). Je potřeba je ještě lépe zpracovat, znát zavedený způsob prezentace dat a metody, jak z nich správně určit jak výslednou hodnotu, tak míru její přesnosti, nejistoty, odchylky nebo jinak i řečeno „chyby“ (každý z těchto pojmů má svůj význam).
Zpracování dat
Poprvé se důkladně zpracováním dat zabývalo 2. Výfučtení 4. ročníku. Z jeho poznámek budeme vycházet, ale rozšíříme je také o obecná fakta, na která už tehdy nezbylo místo, a mírně doplníme některé tehdy zjednodušené pojmy.
Většinou je úkolem určení hodnoty nějaké veličiny. Naši experimentálně zjištěnou hodnotu zapisujeme vždy ve tvaru: veličina=(pravděpodobnáhodnota±nejistota)jednotka, například v=(10,0±0,2)m⋅s−1. O původu pravděpodobné hodnoty a nejistoty si řekneme dále. Platí zde důležitá zásada, že hodnota i nejistota by měly být zaokrouhleny na stejné desetinné místo. Nejistotu navíc zaokrouhlujeme vždy nahoru, protože zaokrouhlením dolů bychom svým výsledkům přisoudili vyšší spolehlivost, než měly (lépe než svou nepřesnost podcenit). Závorky se psát také musí, protože je pak jasné, že jednotka za nimi patří k oběma číslům.
Jako pravděpodobnou hodnotu označujeme právě hledaný výsledek našeho měření. Má-li být výsledkem opakovaného měření veličiny a, její pravděpodobnou hodnotu označujeme jako ˉa nebo ⟨a⟩. Stanovíme ji aritmetickým průměrem jejích jednotlivých naměřených hodnot: ⟨a⟩=a1+a2+⋯+ann, kde n je počet měření. Při měření vzdálenosti pravítkem nebo stálého elektrického proudu ampérmetrem nemá obvykle velký význam provádět opakovaná měření. Pokud ale měříte například průměr válce posuvným měřidlem (šuplerou), je dobré tak učinit v různých osách podstavy a výsledek zprůměrovat.
Sama pravděpodobná hodnota, která je výsledkem našeho měření, může však být více nebo méně vzdálena od skutečné hodnoty, a to o tzv. chybu, která je absolutním rozdílem mezi skutečnou hodnotou a pravděpodobnou (naměřenou). Protože však nikdy neznáme ani skutečnou hodnotu, a tak ani výslednou chybu, namísto pojmu chyba používáme pojem nejistota. Ta, stejně jako chyba, vyjadřuje, jak daleko se může naše naměřená hodnota nacházet od skutečné, ale také je na rozdíl od chyby mírou, kterou jako experimentátoři můžeme stanovit na základě znalosti našeho experimentu – jde o váš poučený odhad vaší vlastní nepřesnosti, tedy (ne)spolehlivosti měření. Uvažte například, že váhami, které mají na sobě od výrobce deklarovánu nejistotu třeba ±150g zvážíte cizí závaží o skutečné hmotnosti 1kg (kterou neznáte) a výsledek, který dostanete od váhy, bude např. 1,1kg. Výsledkem vašeho měření je tedy m=(1,10±0,15)kg se zmíněnou pravděpodobnou hodnotou i nejistotou, avšak chyba, jejíž hodnotu netušíte, činí jen 0,1kg. Je důležité si vštípit, že žádné měření není přesné, tj. každé má nenulovou chybu a nejistotu. Nás při opravování úloh zajímá váš odhad nejistoty jako vyjádření přesnosti měření. Tu lze definovat a určovat několika způsoby a je důležité, jaký si vyberete a také aby to z vašeho řešení bylo zřejmé. Označujeme-li nejistotu veličiny a jako ua, píšeme tedy vlastně náš tvar výsledku výše symbolicky ve tvaru: a=(⟨a⟩±ua)[a].
První veličinu, kterou můžete dosadit na místo nejistot, je tzv. absolutní odchylka, která má význam při malém počtu opakování měření. Δa=|a1−⟨a⟩|+|a2−⟨a⟩|+⋯+|an−⟨a⟩|n Čím vyšší je počet měření, tím ustálenější je hodnota absolutní odchylky.
Poslední zmíněná vlastnost absolutní odchylky však není vždy chtěná, protože stálost pravděpodobné hodnoty i po mnoha měřeních můžeme také chápat tak, že nejistota našeho měření je velmi malá, protože z ní tato hodnota ani na jednu, ani na druhou stranu po mnoha měřeních neuniká. Rádi bychom tedy do nejistoty nějak zaznamenali, kolik měření jsme udělali. To znamená, že v případě mnoha měření, která se nikdy příliš neodchýlila od nějaké pravděpodobné hodnoty, musí být nejistota tím menší, čím více měření jsme provedli. Toto umožňuje definice jiného druhu nejistoty, tzv. směrodatné odchylky σa: σa=√(a1−⟨a⟩)2+(a2−⟨a⟩)2+⋯+(an−⟨a⟩)2n−1. Tato veličina má velký význam ve statistickém zpracování měření a doporučujeme ji univerzálně používat, tedy opět ještě přesněji:9) a=(⟨a⟩±σa)[a].
Nakonec lze u přímých měření používat i jiný typ nejistot, a to nejistoty systematické. Pokud například měříme metrem nějakou délku pevného tělesa či neměnnou vzdálenost, nemá smysl měření opakovat, protože na stupnici s trochou snahy přečteme stále stejnou hodnotu. Co potom ovlivňuje nejistotu? Kvalita měřicího přístroje a naše vlastní práce. V tomto ohledu jsou pro určování nejistot zavedena jistá pravidla závisející na charakteru prováděného měření. Odečítáme-li například hodnotu na nějaké stupnici (metru, váhy, teploměru…), je často bezpečné jako nejistotu položit hodnotu odpovídající velikosti poloviny nejmenšího dílku této stupnice. Některé kuchyňské váhy mají například na jeden dílek přesnost 20g, proto při jejich použití vezmeme nejistotu 10g.10) Jinak je tomu u měření času: jakékoli stopky mají přesnost výrazně vyšší než je postřeh experimentátora, který je řídí. Tento poznatek aplikujeme tak, že stopky považujeme za dokonale přesné, a jako celou nejistotu uvažujeme experimentátorův reakční čas, který je nejčastěji odhadován na 0,2s. Nakonec se nabízí otázka, jak postupovat u přístrojů, které své údaje podávají na digitálním displeji. Každý takový přístroj má na sobě v tomto smyslu řadu různých značení a v jeho manuálu bude také podrobněji popsáno, s jakou nejistotou a za jakých podmínek udává své výsledky. Většinou ale neprohloupíme, pokud budeme také používat přenesenou verzi „poloviny nejmenšího dílku“. Pokud třeba naměříme na voltmetru 4,24V, nejistota je často stále alespoň 0,005V.
U nepřímých měření je mezi výslednou veličinou a vstupními veličinami často známý vzorec, který popíšete už v Teorii (např. v=s/t). Ten lze bez pochyby využít pro výpočet pravděpodobné hodnoty výsledné veličiny (⟨v⟩=⟨s⟩/⟨t⟩), ale jak vypočítat její výslednou nejistotu? Ukazuje se, že nejistoty vstupních veličin nemůžete do daného vzorce jen tak dosadit stejně, jako byste dosadili jejich pravděpodobnou hodnotu (uv≠us/ut). Pokud například délku l na nějaké ose měříte mezi dvěma body se souřadnicemi b a c, platí mezi nimi např. l=b−c, jenže chyba mohla být ve vašem měření b a c na obě strany. Výsledná nejistota l musí být složená z nejistot b a c, protože je stejně pravděpodobné, že jste při měření udělali chybu, která hodnotu l zvětšila, jako že jí zmenšila. Touto úvahou odvozujeme první vzorec pro skládání nejistot: c=a±b⇒uc=ua+ub, pak pro součin a podíl počítáme: c=a⋅b,c=ab⇒uc⟨c⟩=ua⟨a⟩+ub⟨b⟩. Existují i univerzální vzorce pro výpočet nejistot výsledku libovolné funkce jakýchkoli vstupních proměnných. Jejich součástí jsou však tzv. parciální derivace, jejichž výklad by byl zatím značně nadbytečný. Tyto přesné vzorce však odůvodňují například často používaný výsledek výpočtu nejistoty veličiny a, kterou získáváme aritmetickým průměrem bodů a1 až an za podmínky stejné nejistoty ua pro všechny tyto průměrované body: uprůměr=ua√n. Tento vztah také ukazuje, že správně definované nejistoty se snižují s větším množstvím měření. V první kapitole o teorii jsme zmínili, že opakovaná měření vedou k vyšší přesnosti, protože podělením součtu dělíme i nejistotu. To je založeno na vztahu: a=K⋅b⇒ua=K⋅ub, kde K je nějaká číselná konstanta bez jakékoli nejistoty. Při dělení počtem měření odpovídá 1/n.
Poznámka: Pokud náhodou násobíte tři veličiny, jako například při výpočtu objemu ze tří naměřených rozměrů, můžete počítat nejistotu objemu stejně jako při součinu dvou veličin, jen budou ve vzorci vystupovat 3 sčítané zlomky.
Ještě k pojmům: slovo nejistota používá méně lidí, protože se často zaměňuje skutečná a pravděpodobná hodnota měření (v praktickém životě někdy postačí jako skutečnou hodnotu označovat výsledek daný měřicím přístrojem výrazně vyšší přesnosti, se kterým můžeme naše měření kontrolovat). Proto budete často slýchávat a někdy i číst v odborném textu na místě nejistot o chybách nebo odchylkách (často protože se jako nejdůležitější veličina nejistoty používá směrodatná odchylka). Tímhle zdánlivým zmatkem se nenechte odradit. Chyby navíc můžeme (pokud bychom je znali) zpracovávat stejnými matematickými vzorci jako nejistoty. I proto můžeme doporučit si přečíst i další Výfučtení „Sliby chyby“ z 4. série 1. ročníku, kde můžete najít také další vztahy pro výpočet nejistot/chyb nepřímých měření.
Grafy
Někdy však nemusí být cílem experimentální úlohy určit nějakou hodnotu, ale nalézt „závislost“ mezi dvojicí veličin. V těchto případech je obvykle nutné nakreslit graf, do kterého zaznamenáme body odpovídající naměřeným hodnotám a hodnotám veličiny, na níž by měla ta měřená veličina záviset. Příklad grafu je na obrázku: jde o graf závislosti veličiny h měřené v cm v závislosti na m, měřené v gramech. V tomto grafu se zvolila červená pro jednotlivá měření a zelená pro přímku, která vychází z teoretického výpočtu, abychom viděli, že teorie dobře odpovídá skutečnosti.
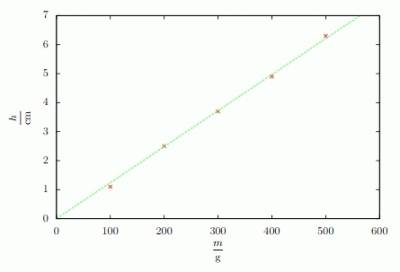
Prakticky je jakákoli grafická úprava (ať už počítačového nebo ručně rýsovaného grafu) vhodná, ale vždy musí být splněny určité náležitosti:
- Musí být jasné, které ose odpovídá která veličina a také v jakých jednotkách je každá veličina vyjádřena – v těchto jednotkách poté musí být i číslování os. Nezávislá proměnná je vždy na vodorovné ose.
- Popisky os grafu by měly být jednoznačně umístěny tak, aby bylo zřejmé, ke které z os se vztahují (například v levém dolním rohu začínají obě osy, proto jde o nevhodné místo).
- Hustota dílků (a jejich popisků) by měla být přiměřená a zrovna tak zvolené meze. V obr. 1 by například nebylo vhodné zdesetinásobit počet rysek na vodorovné ose, když jsou známé body měření příhodně po 100g. Stejně tak by bylo nevhodné vodorovnou osu prodloužit až do 1000g nebo svislou do 10cm, protože pak by naměřené hodnoty rovnoměrně nepokrývaly plochu grafu – bylo by zde nevyužité místo a také by se zhoršila čitelnost, pokud by byl zmenšený.
- Datové body (výsledky měření) jsou správně výrazné, nejlépe barevně odlišené.
Při úkolu „nalezení závislosti“ nás nejvíce potěší, pokud určíte i typ funkce, která dané dvě veličiny váže. Zda je lineární, kvadratická nebo třeba hyperbolická (s mocninou −1). Tyto funkce můžete zapisovat také obecně za použití různých neznámých konstant. Z obrázku lze například vyčíst, že mezi h a m asi existuje lineární závislost, která se dá spolu s nějakými ještě neznámými konstantami d a e zapsat h=d⋅m+e. Postupu hledání funkčních závislostí se říká fitování a jeho matematická metoda se nazývá regrese. Více se o ní můžete dočíst ve Výfučtení „O kráse regrese“ 5. série 1. ročníku. Nicméně už i takto obecně zapsaná je taková závislost odpovědí na otázku úlohy.
Závěr
Kromě výše popsané náplně závěru (konečné výsledky, kvalita měření, návrhy na zlepšení, příp. porovnání se známými/tabulkovými hodnotami) můžeme dodat – nebojte se nešetřit s komentáři svého měření. Co výsledky znamenají a jak vaše měření probíhalo či neprobíhalo je cennou informací pro další dobré experimentátory. Vyhněte se například komentářům typu „chyba byla malá/velká“ nebo dokonce „v rozumných mezích“. Takové soudy nemají fyzikálně žádný význam, protože, jak zkušenost ukazuje, jsou často i mylné. Namísto toho se snažte říkat jen to, co můžete dokázat číselně; jak se říká „jen to, co můžete změřit-zvážit.“ V tom je nejdůležitější poučení teorie nejistot a chyb.
Úplný závěr
Z vlastních zkušeností můžeme říci, že experimentování rozhodně není jednoduchá záležitost. Vyžaduje především spoustu času, který musíte věnovat hlavně přípravě a poté zpracování měření. To většinou tvoří jen několik procent celkového času. Měření dat bez přípravy a náležitého zpracování pozbývá významu. Práce fyzika není jen o hraní si s přístroji, ale hlavně o jejich nastavení. Doufáme, že vás náš text pomůže navést k vytvoření správného a efektivního způsobu, jak budete vaše měření zpracovávat. Můžete si vytvořit osnovu, podle které budete pokaždé postupovat, což výrazně urychlí vaši práci. Doporučujeme si přečíst starší vzorová řešení experimentálních úloh, která naleznete v archivu na našich webových stránkách. Všimněte si zároveň i poznámek k došlým řešením, které vám mohou dopředu poradit, čeho se máte vyvarovat nebo co naopak udělat, abyste dosáhli lepšího hodnocení.
Na závěr vám přejeme hodně štěstí, trpělivosti a pečlivosti, která se určitě nakonec vyplatí. S případnými dotazy nás neváhejte kontaktovat na vyfuk@vyfuk.org. Pokud se chcete o problematice zpracování měření dozvědět více, navštivte experimentální sekci našeho bratrského středoškolského semináře FYKOS: http://fykos.cz/sex/jak-na-to. Kromě jiného si zde můžete přečíst i něco o pokročilém zpracování dat. Velmi užitečný (zato pro nás velmi nadstavbový) studijní text byl napsán pro řešitele Fyzikální olympiády: http://fyzikalniolympiada.cz/texty/mereni.pdf. Přehledně zde najdete popsaný především složitější postup zpracování dat, který využijete právě při řešení olympiády, FYKOSu a dokonce i na vysoké škole.